Multi variable linear regression

4. Multi variable linear regression

: 여러 개 입력(feature)의 Linear regression

 

- 하나의 input variable

one-variable

Hypothesis

: H(x) = Wx+b

: W와b 를 학습

 

Cost function

 

Gradient descent algorithm

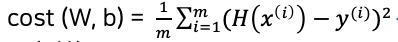
gradient descent algorithm

 

 

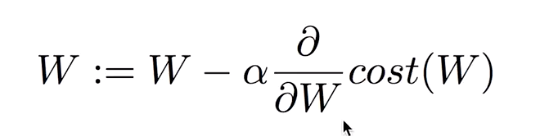
- 여러 개의 input

multi-variable/feature

ex> 시험을 보는데 시험1,2,3 의 결과를 가지고 final 시험 점수를 예측(input 3개)

: H(x1,x2,x3) = w1x1 + w2x2 + w3x3 + b         //예측

 

cost(W,b)

 //예측 값과 실제 값의 차이의 제곱의 평균

                         

- n개가 된다면,

: w1x1 + w2x2 + w3x3 + ... +wnxn

: 복잡해지고 길어지므로, Matrix(행렬) 사용

 

 

- Matrix multiplication(행렬의 곱) 사용

matrix multification

: X 와 W 순서는 바뀌어도 됨

: X 는 매트릭스를 뜻함

: 따라서 매트릭스에서는 XW 으로 표현

 

 

matrix multification

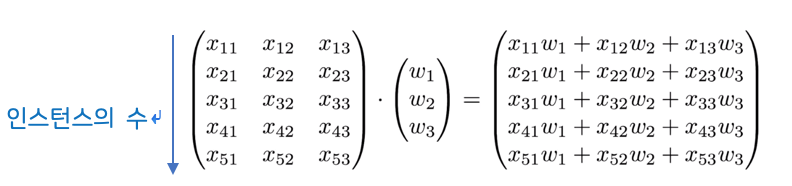
: 매트릭스를 쓰는 또다른 장점은,

: W 는 변화가 없고 인스턴스가 많을 때 각각의 인스턴스를 계산할 필요 없이

 전체를 긴 매트릭스에 넣고 그냥 W 를 행렬 곱을 하면, 원하는 값이 나옴 

 

: 인스턴스 입력5개, feature 3개(variable 3개)

 [5,3]   [3,1]    =   [5,1]  이 되는 것

             [5,3]                         [?,?]                             [5,1]

일 때,  W 가[3,1] 인 매트릭스 임을 예측 가능
                                                     

: 매트릭스를 사용하면 이렇게 

multi variable의 경우에도, 

인스턴스가 많은 경우에도, 

출력이 여러 개인 경우에도 쉽게 처리할 수 있음

 

- 이제는x 가 하나가 아니라 여러 개 일테니까 매트릭스를 많이 사용하게 될 것,

주의할 점

theory 에서는 

H(x) = Wx + b 

                           이지만,

 

실제 사용(구현)에서는(Implementation, Tensorflow)

H(X) = XW 

                           를 사용.

 

 

 

 

출처 : 모두의 딥러닝 https://hunkim.github.io/ml/