3. Linear Regression cost 함수 최소화

가 최소값을 가지도록 하는 W,b 를 구하는 것이 목표!
설명을 위해 Simplified hypothesis 를 예시로 듦
H(x) = Wx (b=0 으로 봄)

data set :
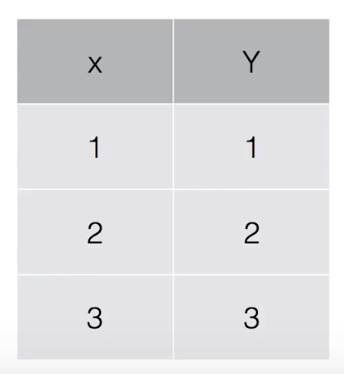
: W=1, cost(W) =0

: W=0, cost(W) =4.67
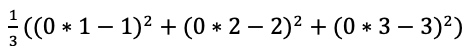
: W=2, cost(W) =4.67

...
-> 함수를 그려보면,
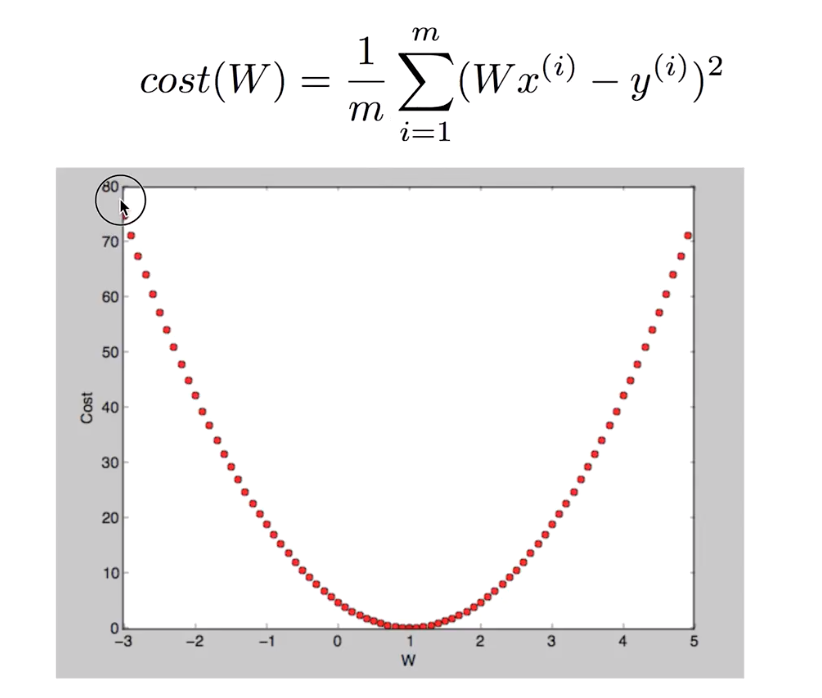
: 목표는 cost 가 0이 되는 점을 기계적으로 찾아내는 것
-> cost function 을 minimize하는데 많이 용되는 알고리즘이
Gradient descent algorithm
: 머신러닝, 또는 이외의 minimization problems 에 사용
: cost값이 하나가 아니라 W1,W2,W3..일 경우에도 사용
Q. 어떻게 한 지점에서 가장 lowest 한 point 를 찾을 수 있을까?
A. Gradient descent algorithm 을 이용,
어떠한 지점(0,0도 가능) 에서 경사도를 따라 한 발짝씩 움직여 (W를 조금씩 바꾸어) 경사도가 0인 곳을 찾음
Q. 경사도는 어떻게 구할까?
A. 미분을 통해 구함
formal 한 정의를 위해 (미분식을 깔끔하게 만들기 위해)

를 사용, (미분하면 값 동일)
그리고 W 에는

의 값을 넣음
알파 : 0.1의 값을 가지는 상수
따라서 미분의 공식을 적용해 미분을 거치면,

: 이렇게 최종적인 알고리즘이 완성
: 여러번 실행을 시키면서 W 값이 바뀌고,
cost 를 minimize 하는 W 값이 자동으로 구해지는 것

: 이 그림 예시를 보면 어느 점에서나 시작해도 된다는 가정에 따라 출발을 해 minimize 되는 값을 찾아내면 둘의 값이 다름
: 다행히도 우리의 가정을 가지고 cost function 을 그리게 되면,

: convex (볼록) 의 형태를 띄며 gradient 알고리즘이 항상 답을 찾는다는 것을 보장함
: 따라서 Cost function 을 설계할 때 반드시 모양이 convex 의 모양을 띄는지 확인해야함
- 기울기 하강 최적화(Gradient Descent Optimization)
출처 : 모두의 딥러닝 https://hunkim.github.io/ml/
'AI & Deep Learning > 이론' 카테고리의 다른 글
| Logistic Classification (Binary) (0) | 2019.04.01 |
|---|---|
| Multi variable linear regression (0) | 2019.04.01 |
| Linear Regression 의 개념 (0) | 2019.04.01 |
| tensorflow 의 기본 (0) | 2019.04.01 |
| 머신 러닝의 개념 (0) | 2019.03.31 |



